By Santiago Mondragon
July 25, 2024
Over the past few months, I have been working on warehouse software used by a distributor to track shipped out products. The warehouse uses handheld barcode scanners to scan the serial numbers of the products they will ship out. One problem we encountered recently is that sometimes the barcode scanner will do an incomplete scan of the serial number. It would be extremely inconvenient (almost impossible) for the person scanning the serials to ensure that the scanner scanned the full serial because they have to scan hundreds to thousands of serials per day. I was discussing this issue with the warehouse manager, brainstorming ways to detect when such cases occurred. We initially discussed sorting the serials by length so that incomplete serials would be at the top. This would make it easier to find incomplete serials that were missing a substantial portion, but not for those which might only be missing one or two characters. To complicate things further, products of the same model could have different lengths when they come from different boxes (but always the same length within the same box), so we couldn't just check for a specific length and call it a day. At first I was stumped on how I could write a detector for such cases. After doing some research, I found my solution: approximate string matching aka fuzzy string matching.
Fuzzy string matching is a technique used to match two strings even when they are not exactly the same. This is done by computing the similarity between the two strings. One measure of similarity between strings is the edit distance. The edit distance is calculated by adding up the number of insertions, deletions, and substitutions required to get from the first string to the second. The edit distance can be thought of as the cost to convert one string to the other. Strings with lower edit distances are more similar than strings with higher edit distances. There are different ways to compute the edit distances such as Levenshtein distance, Damerau-Levenshtein distance, and Hamming distance. The difference between the various distances is what kind of operations are allowed when converting one string to another.
In our case, we only need the replace operation (swapping out one character for another) since serial numbers that belong to the same box always have the same length of characters. The Hamming distance is perfect for this as it only allows replacement operations. Strings that are not the same length will automatically be given a score that reflects that they are not similar even if one string where to be a substring of the other. Let's say we have three serial numbers: SN001, SN003, and 120AC. Below is how we would calculate the similarity between SN001 to the other two serial numbers using the Hamming distance.
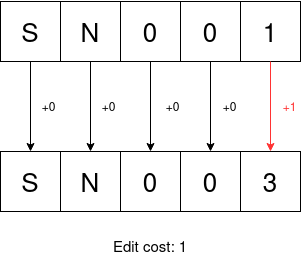
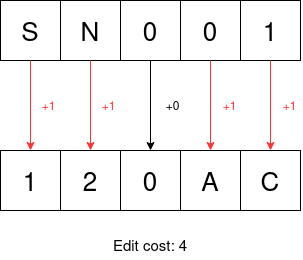
As you can see, SN003 is more similar to SN001 than 120AC is.
The Hamming distance gives the same weight to all replacements. For our purposes, we would like to give more weight when replacing a letter with a digit or a digit with a letter because this happens less with serials of the same box. For example, let's say that the serials have the following format:
Start with 'SN' and increment the digits for each itemSN001, SN002, SN003, SN004, SN005, SN006, SN007, SN008, SN009, SN010If we then encounter a serial that starts with digits instead of SN when scanning this box, it is probably an incorrectly scanned serial and the user should be alerted. I modified the Hamming distance algorithm so that the cost for a replacement is the difference between the ASCII value of the character being replaced and the ASCII value of the replacement character. The edit distance diagram now looks like so:
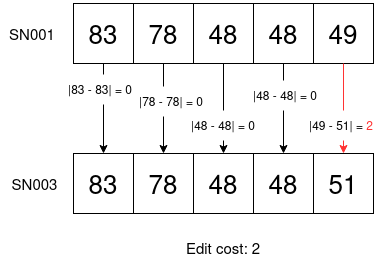
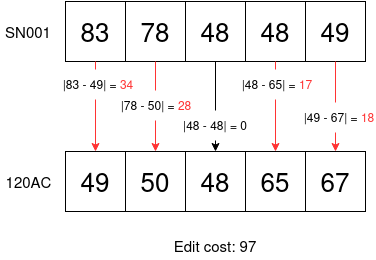
Now we can see that there is a much bigger difference in edit cost when comparing SN001 to 120AC than when comparing it to SN003.
Below is the the Hamming distance algorithm in Python:
def get_hamming_distance(serial1, serial2, THRESHOLD):
"""Return the hamming distance between two serials"""
if len(serial1) != len(serial2):
return THRESHOLD + 1
return sum([abs(ord(char1) - ord(char2)) for char1, char2 in zip(serial1, serial2)])
In order to choose the threshold that would lead to the highest accuracy, I wrote a script that tried different thresholds on over 700,000 serial numbers already in the database. I found the best threshold to be:
THRESHOLD = LENGTH_OF_SERIAL_NUMBER * 6
Using this equation for the threshold led to an accuracy of over 99.95% for detecting incorrect serials and not raising false positives on the 700,000 test serials.
Below I use the hamming distance to search for incorrect serials on an actual Sales Order. For each serial number, I try to find a least one other serial that is within the threshold. If there is no serial that is similar enough, that serial is presented to the person scanning the serials because there is a high probability that it is incorrect scanned. All 1600 serials in this order are correct, so I manually replaced one with 120AC123 (length 8 since all serials in the list are length 8) so that there would be one incorrect serial detected.
import timeit
import pandas as pd
def find_incorrect_serials(serials, threshold_multiplier):
"""Return a set containing invalid serials"""
invalid_serials = set()
if len(serials) > 1:
for sn in serials:
THRESHOLD = len(sn) * threshold_multiplier
is_valid = False
idx = 0
while not is_valid and idx < len(serials):
sn2 = serials[idx]
idx += 1
if sn != sn2:
dist = get_hamming_distance(sn, sn2, THRESHOLD)
if dist < THRESHOLD:
is_valid = True
if not is_valid:
invalid_serials.add(sn)
return invalid_serials
if __name__ == "__main__":
THRESHOLD_MULTIPIIER = 6
sales_order = pd.read_csv('sales_order.csv')
serials = sales_order.loc[:, 'Serial Number']
start = timeit.default_timer()
invalid_serials = find_incorrect_serials(serials, THRESHOLD_MULTIPIIER)
stop = timeit.default_timer()
print('Invalid:', invalid_serials)
print('Serials checked: ', len(serials))
print('Time: ', stop - start)
$ python detect_incorrect_serials.py
Invalid: {'120AC123'}
Serials checked: 1600
Time: 0.016168985999684082
As mentioned above, I ran the algroithm on over 700,000 serial numbers to find what threshold would lead to the highest accuracy. Below are some of the results of the different threshold multipliers.
Threshold multiplier: 6
Error: 331
False positives: 119
False negatives: 212
Total serials checked: 733810
Accuracy: 99.95489295594227%
real 6m24.637s
user 0m13.944s
sys 0m0.242s
Threshold multiplier: 1
Error: 100837
False positives: 100827
False negatives: 10
Total serials checked: 733810
Accuracy: 86.25843201918752%
real 17m3.014s
user 10m50.661s
sys 0m0.176s
Threshold multiplier: 7
Error: 386
False positives: 58
False negatives: 328
Total serials checked: 733810
Accuracy: 99.94739782777559%
real 6m16.092s
user 0m5.492s
sys 0m0.197s
Threshold multiplier: 10
Error: 546
False positives: 15
False negatives: 531
Total serials checked: 733810
Accuracy: 99.92559381856339%
real 6m13.289s
user 0m3.234s
sys 0m0.172s